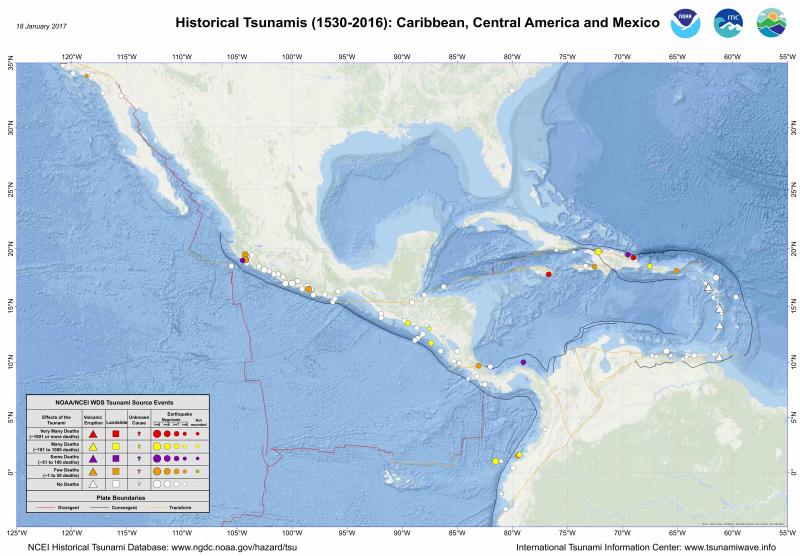
El tsunami es uno de los fenómenos naturales más destructivos. Como ejemplos recientes se encuentran los tsunamis de Sumatra-Andaman en 2004 que provocó la muerte de 283 000 personas en las costas del océano indico y el de Japón en 2011 con 16 000 muertos aproximadamente, provocados por dos terremotos de grandes proporciones. Los sistemas de alerta temprana ante la ocurrencia de un tsunami tienen como uno de sus objetivos principales conocer, en el menor tiempo posible, la potencialidad de los terremotos para generar tsunami. La fase W fue propuesta por Hiroo Kanamori (1993) después del tsunami ocurrido en Nicaragua en 1992 (que cobró la vida de 170 personas), es una onda de cuerpo de largo período que se propaga rápidamente (entre la onda P y la onda S) lo que permite la estimación oportuna de la información básica de la fuente sísmica (mecanismo focal, momento sísmico, magnitud, ubicación del centroide y duración de la ruptura) como parámetro de entrada para estimar entre otra información, el tiempo de propagación de las olas de tsunami en el mar, dispersión de la energía y la altura de las olas que potencialmente pueden arribar a las costas.
Expositores
Aula CESEM
Segundo nivel edificio T-1
Ciudad Universitaria, USAC. Zona 12
