Integral de Lebesgue e Integral de Daniell
Aula virtual
Segundo nivel edificio T-1
Ciudad Universitaria, USAC. Zona 12
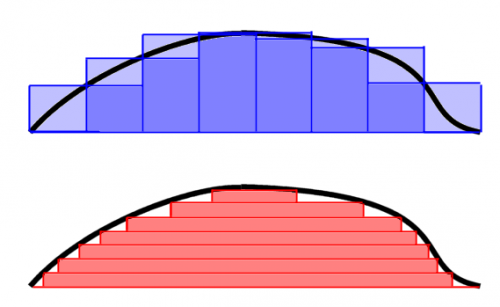
En matemáticas, la integral de una función no negativa de una sola variable puede considerarse, en el caso más simple, como el área entre la gráfica de esa función y el eje x. La integral de Lebesgue extiende la integral a una clase más grande de funciones. También amplía los dominios en los que se pueden definir estas funciones.
La integral Daniell es un tipo de integración que generaliza el concepto de versiones más elementales tales como la integral de Riemann. Una de las principales dificultades con la formulación tradicional de la integral de Lebesgue es que requiere el desarrollo inicial de una teoría de la medida viable antes de que se puedan obtener resultados útiles para la integral. Sin embargo, un enfoque alternativo está disponible, desarrollado por Percy J. Daniell (1918) que no sufre de esta deficiencia, y tiene algunas ventajas significativas sobre la formulación tradicional, especialmente en como la integral se generaliza a espacios de dimensiones superiores y otras generalizaciones tales como la integral de Stieltjes. La idea básica consiste en la axiomatización de la integral.